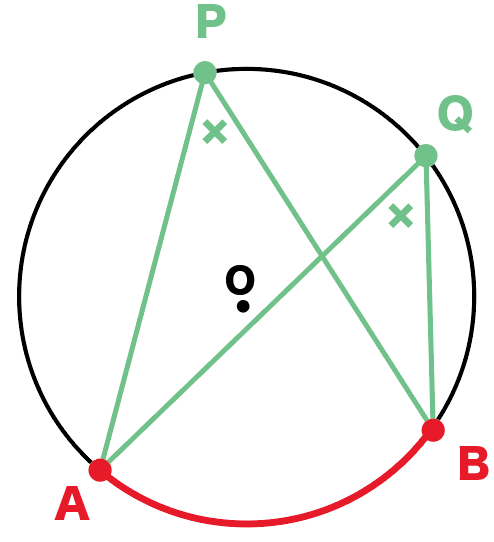
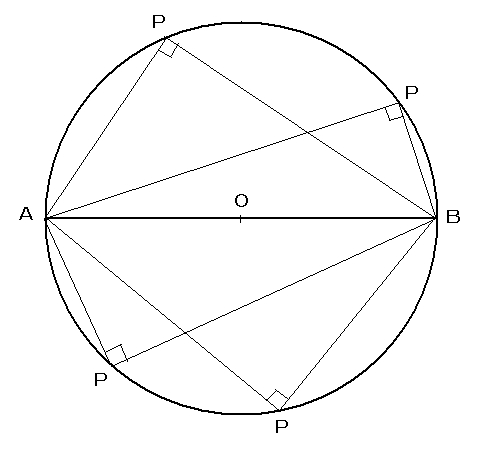
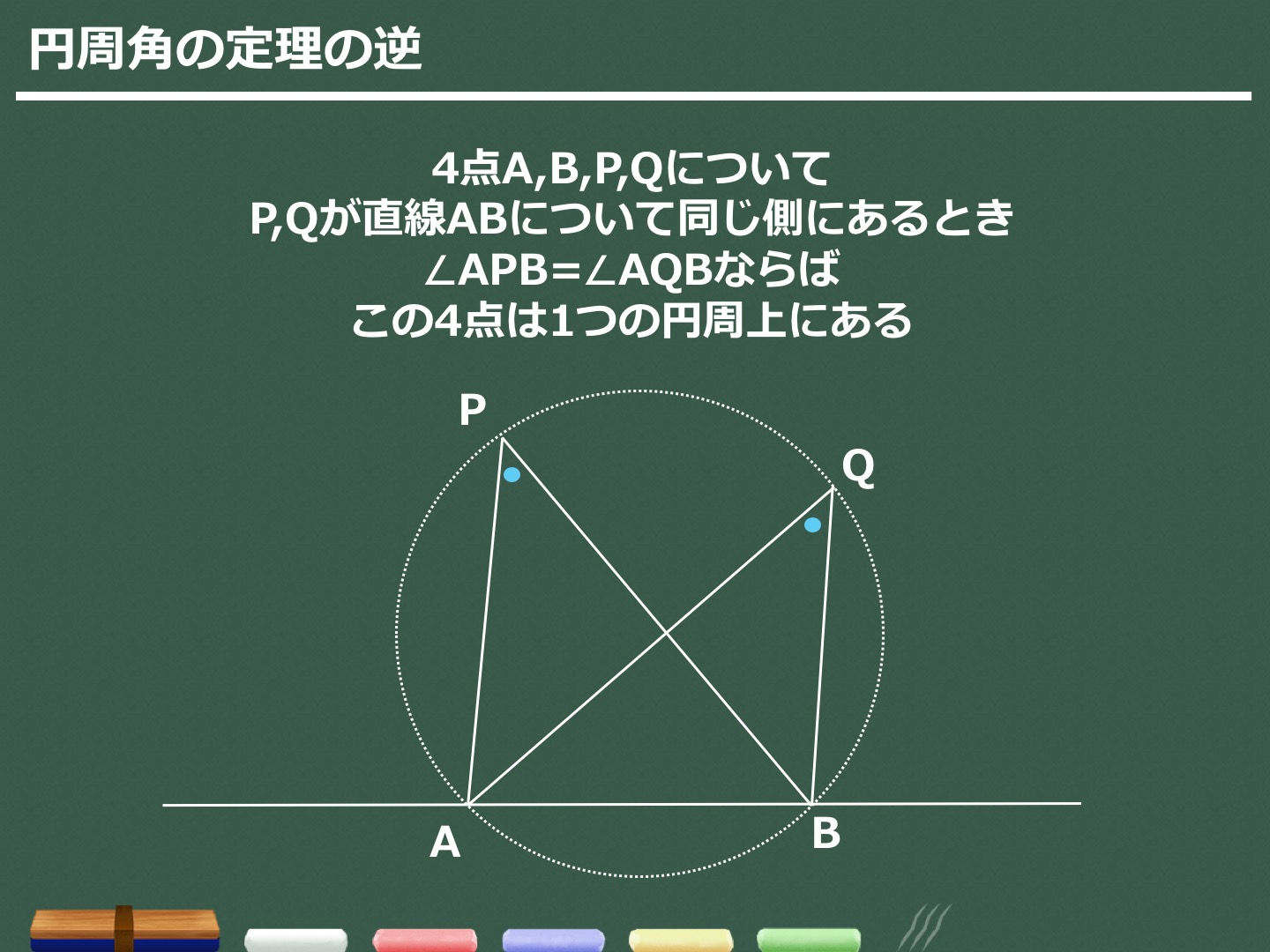
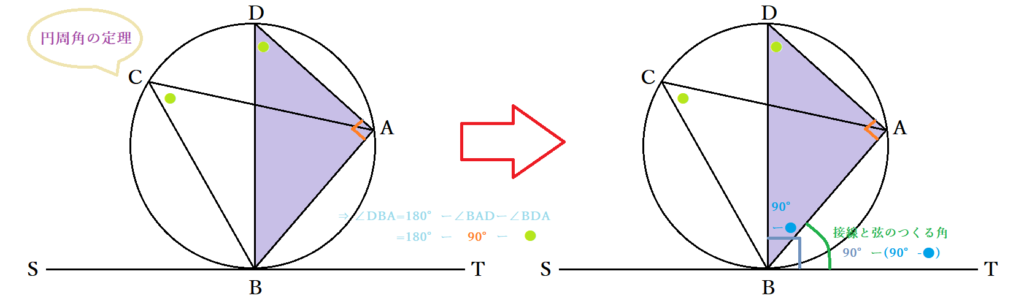
「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。 接弦定理は、 ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が少しずつ変わってきます。円周角の定理「 1 つの弧に対する円周角は一定」 を利用して, 角度が等しいときにその 2 つの角をつくる 4 点が同一円周上にある ことを証明していきます。 円周角の定理の逆は, 2 点 , が直線 について同じ側にあるときに が成り立つならば, 4 点 , , , は1つの円周上にある。直径は180°という角度になるということをしっかりと覚えましょう. また 「直径の上に立つ円周角は直角になる」 は重要定理ですからすぐに使えるように覚えておきましょう.

円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学
円 角度 定理 接線
円 角度 定理 接線-円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは,a c = 180 を説明 (証明)します。 円 周 角 : に 対 円に内接する四角形の性質とその証明まとめ 円に内接する四角形の性質を整理しました。円周角の定理からトレミーの定理まで,全部使えるようになっておきましょう! → 円に内接する四角形の性質とその証明まとめ



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
図形・円 中学数学円周角の定理 導入 中学数学円周角の定理はなぜ成り立つのか 中学数学円周角の定理 例題その1 中学数学円周角の定理 例題その2 中学数学円周角の定理 例題その3 中学数学円周角の定理 例題その4なるよう定理や公式の重要度を以下のようなa,b,c,d の4 段階に分けてあります。 a 志望校を問わず全ての受験生が知っておくべきレベル(おそらく学校でも習う) 凹四角形の角度の関係 a x = 4 角の二等分線に関係する辺の比や長さ b 内接円を利用(ア) opaで,op=oa(半径)だから,・・・・1 ∠aob=∠opa+∠oap(三角形の外角) 1,2より したがって ∠apb=1∠aob 2
タレスの定理 (タレスのていり、 英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理 、 タレースの定理 ともいう。== 円周角の定理1 == 元のHTML教材 URLhttp//wwwgeisyaorjp/~mwm461/math2/cir101htm PDF版 問題cir101qpdf 解答cir101apdf 戻る 「 \(4\) 点の位置関係と角度から、それらが同一円周上にあることを示す 」のが、円周角の定理の逆ということですね。 円周角の定理の逆は証明問題で使うこともあれば、角度を求める問題であと一歩ヒントが欲しいときに活用することもあります。
4 第1 章 曲線 k = 3, r = 1 k = 5=3, r = 1 k = 3, r = 1, l = 1 2 k = 5=3, r = 1, l = 3 2 例119 エピトロコイド(epitrochoid, がいよはいせん 外余擺線) は次の径数表示で与えられる曲線で ある。半径r の円が半径kr の円周に外接しながら滑ることなく転がるとき、動円の中心 から距離lr にある定点が描く軌跡であ 三平方の定理より、 AC^2 = 28^2 44^2 AC = 522 cm 円Oの中心点Oを使って三角形ABCを3分割する。 三角形ABC = 三角形OAB 三角形OBC 三角形OCA 円Oの半径をxとして、三角形の面積の公式に当てはめる。 44*28/2 = 28x/2 44x/2 522x/2 616 = 621x x = 99cm 円周を求める 99 * 2 * 314内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



円周角
2 円周角の定理は2つある 21 中心角の半分が必ず円周角になる 22 弧の長さが同じ場合、必ず円周角は等しい 3 弧が半円の場合、円周角は90°になる つまり, 向かい合う内角の和が 180^ {\circ} 180∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。 性質1' こんにちは!レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 19年の大阪教育大学附属高等学校平野校舎の過去問より。 円周角の定理を使った良い問題だと思います。 持っている知識を生かして柔軟に考えてみて下さい! ヒント 答え 詳しい解説 ① 状況把握 ②



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
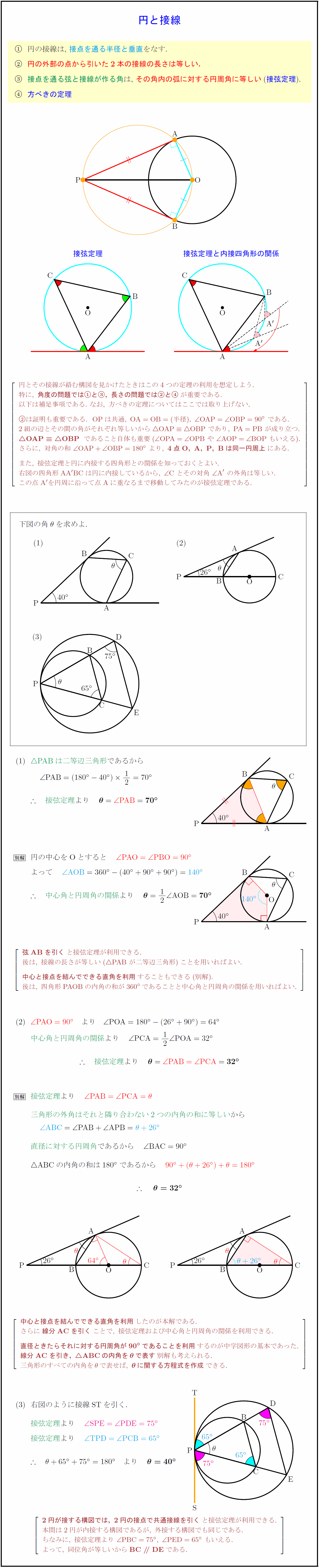



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
定理一覧 円を含む図形 方べきの定理 トレミーの定理 シムソンの定理 シュタイナーの定理 アルハゼンの定理 ニュートンの定理 九点円の定理 フォイエルバッハの定理 ターレスの定理 パスカルの定理 アポロニウスの定理 ブリアンショの定理Title FdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date 接弦定理 接弦定理 は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。 次のような状態の時ですね。 三角形が円に「内接」しているのがわかります。また円に接線が書いてあり、その接点が三角形の頂点に




数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 二等辺三角形の2つの底角は等しい. (2) 円周角は中心角の半分になる.(円の定理に関する証明は全て、「余談」として見てくださいね! 定理(武器)を使って、「値」を求める問題がほとんどですので! ですが「原理」を納得することも大切ですので、できる限り証明していきますね!) 『 接点までの距離は等しい 』 円の外に円周角と弧の比2 円周角は弧の長さに比例する。 三角形の外角は それと隣り合わない2つの内角の和に等しい。



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
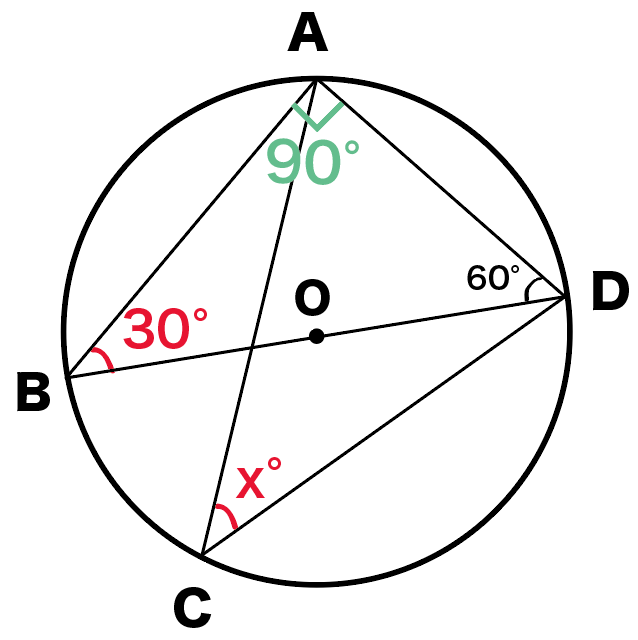
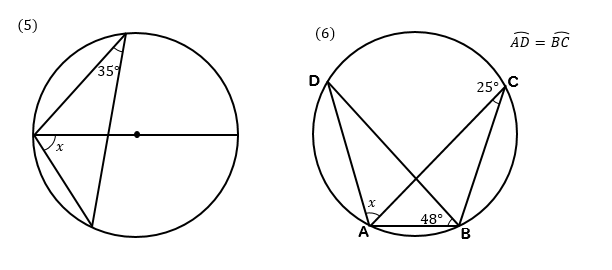
円周角は中心角の半分→中心角は円周角の 2 倍 x = 24 ° × 2 x = 48 ° 2:32 (4) 弧 (オレンジ色)の中心角は 360 ° − 150 ° = 210 °円関数から加法定理へ - 三角関数諸公式への見通し - 札幌東高等学校 大山 斉 観覧車のように回転によって位置が決められる場合がよくある。 回転運動は点が円周上を運動することについて調べていけば良い。 まず回転を表す量として角度が導か①自由度1,グループ1124(𝑥 = 114) 証明の概略 adに関して cと対称な点eをとる aceは正三角形かつ b,d,eは一直線に並ぶ ∠abe=2∠aceより a,b,eを通る円の中心は cである 円周角の定理より ∠acb=2∠aeb=48° 17 18



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく




円周角の定理とは 必ず押さえたい7つのポイント 遊ぶ数学
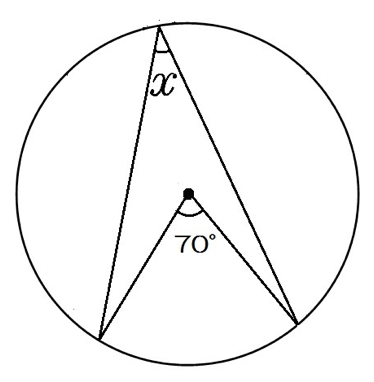
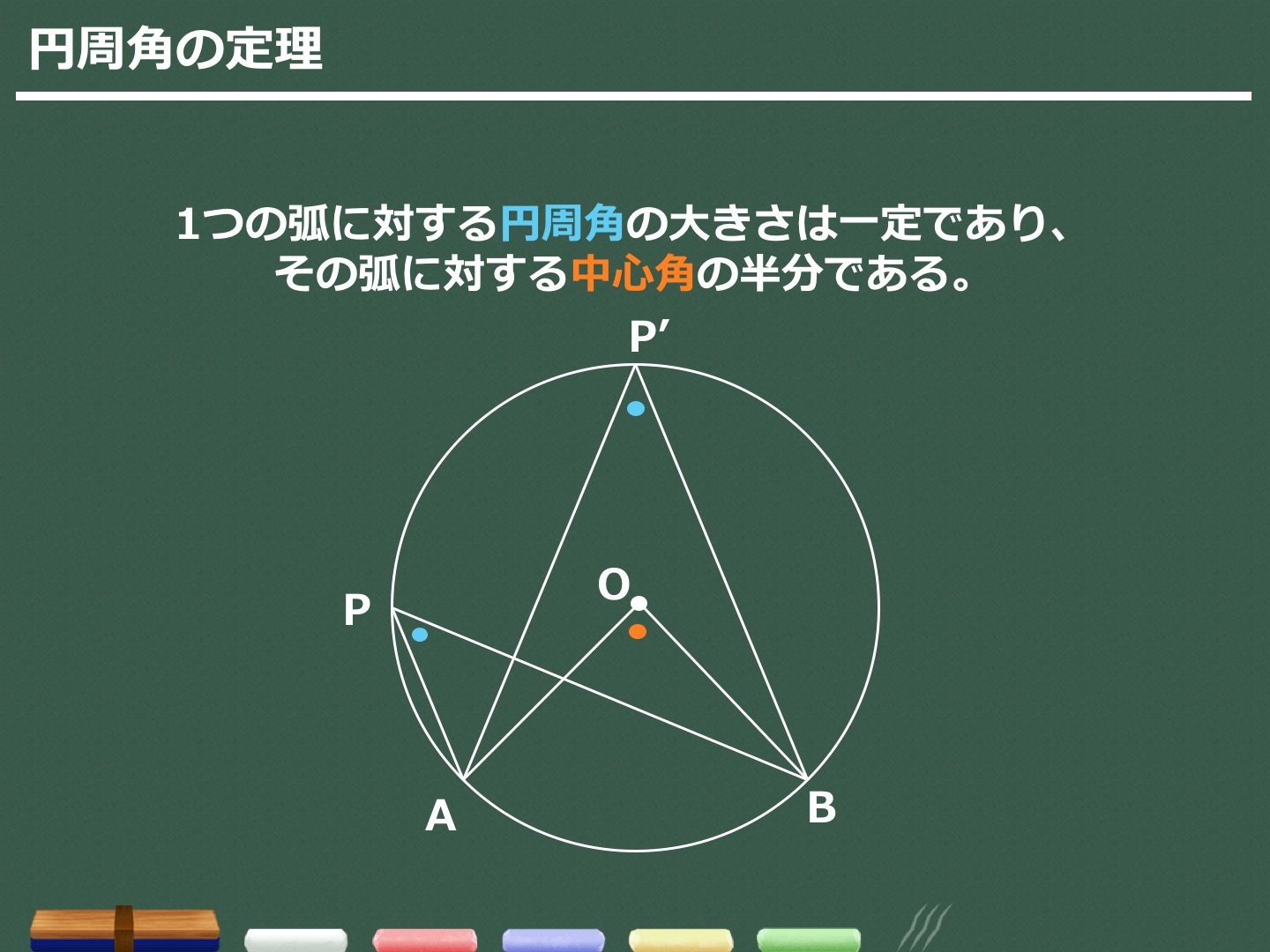
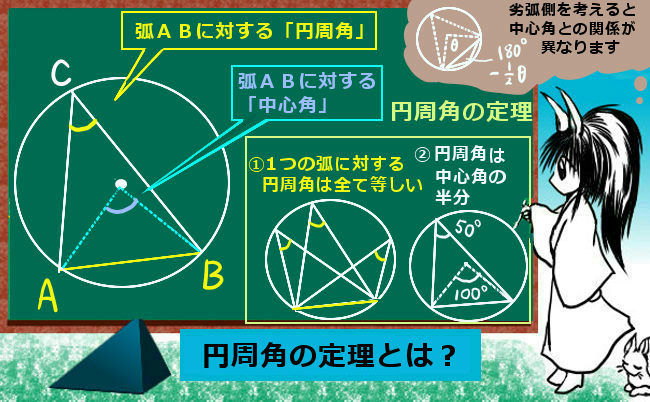
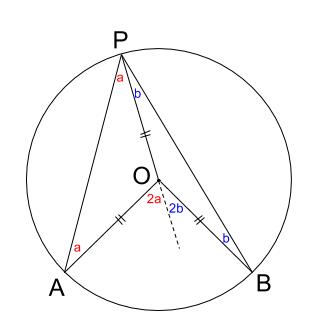
数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠ACB=∠ADB ・∠AOB=2∠ACB=2∠ADB また、次の図のよの辺で重ね,これを半径2cmの円周上 に置く。 ※各頂点が円周上にピッタリと収まることに気がつく 。 る。円周を等分する円周上の6点から任意 図1 図2 なお,円周角の定理と3平方の定理により,辺の長 さはすべて求めることが可能である。 円周角の定理の証明の3パターン 「円周角の定理」を証明していくぞ。 3点a・b・pがある円oを想像してくれよな。 円周角と中心角の位置関係はつぎの3通りある。 点 pがob上にあるとき;



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ
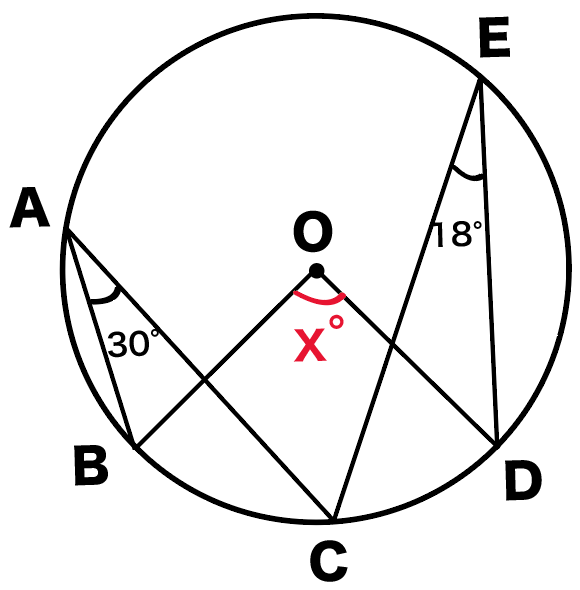
円周角の定理より C 3 = α/2 である。 円周角 (えんしゅうかく)とは、 ユークリッド幾何学 においてある 円周 上の一点から、この点を含まない円周上の異なる二点へそれぞれ 線分 を引くとき、その二つの線分のなす 角 のことである。




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




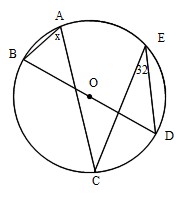
Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理はこれで完璧 定理の証明と様々な問題の解法




円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張




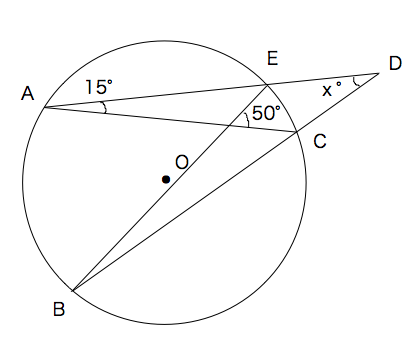
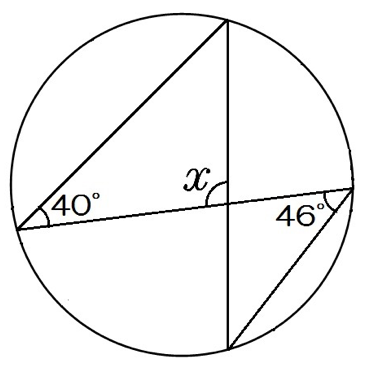
この2つの問題の角xの部分の解き方と答えを教えてください Clear




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
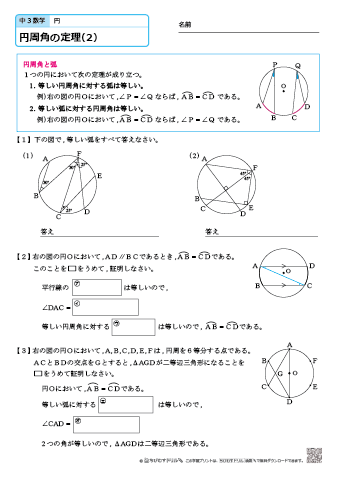



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円周角の定理 角度の計算方法と中心角 弧の長さの関係 リョースケ大学




接弦定理の証明 円周角が鋭角ver 数学a By となりがトトロ マナペディア
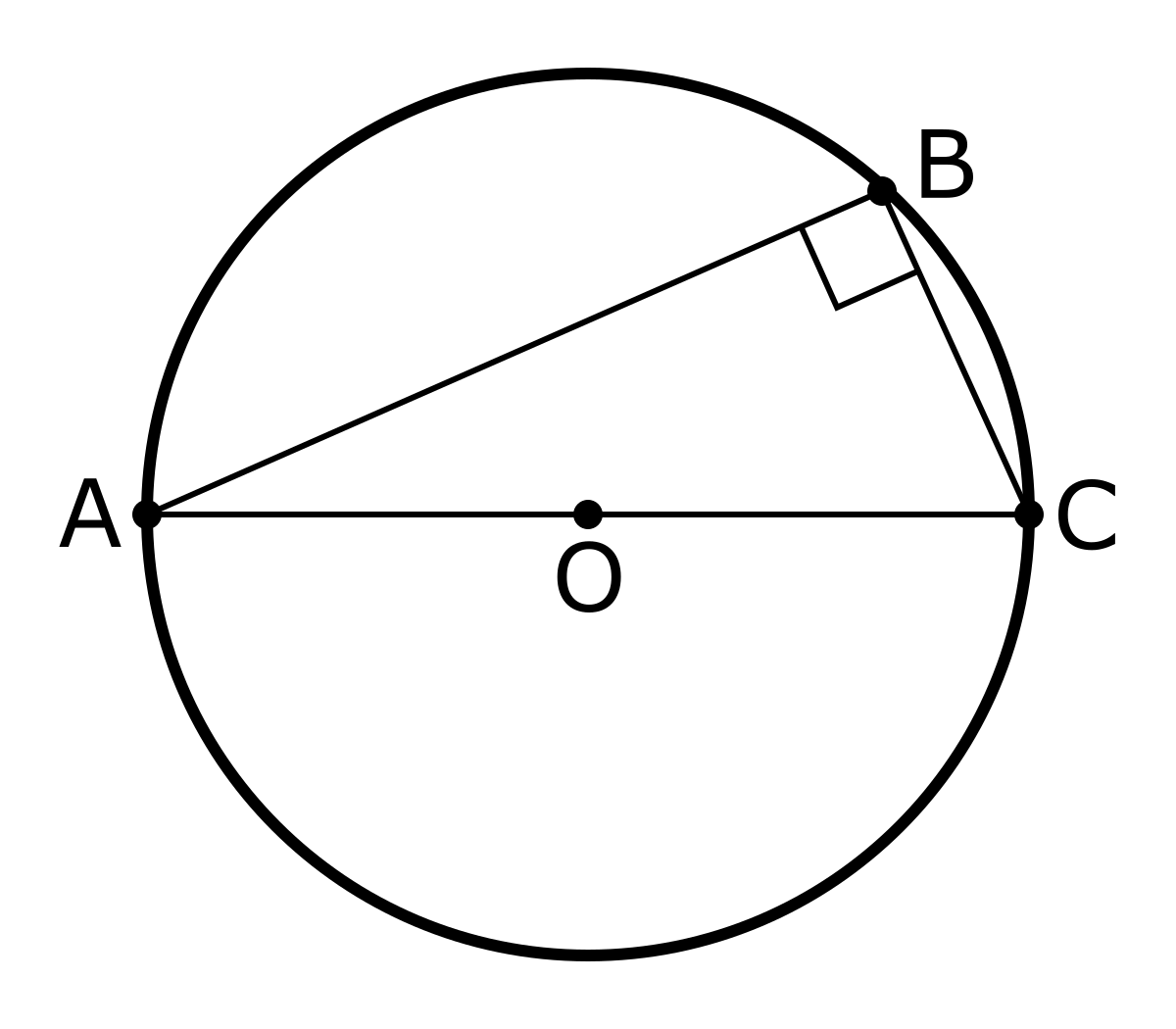



タレスの定理 Wikipedia
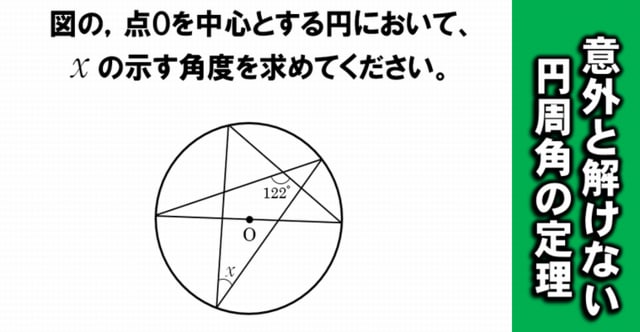



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ
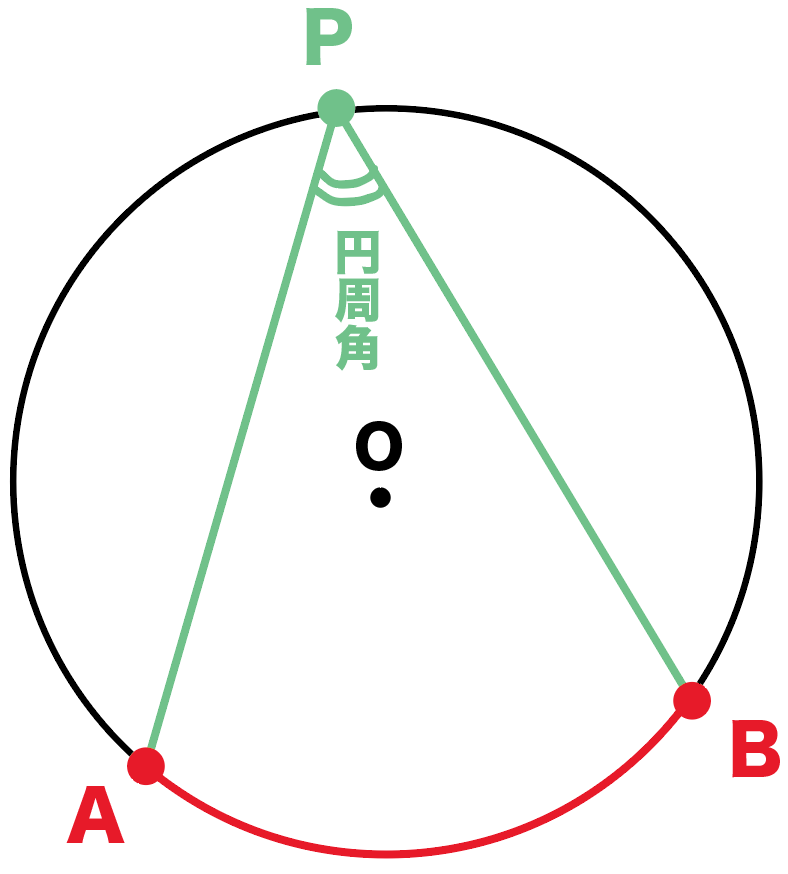



3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく




中学数学 円周角 中心角



タレースの定理




円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



円周角の定理 理数系無料オンライン学習 Kori



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
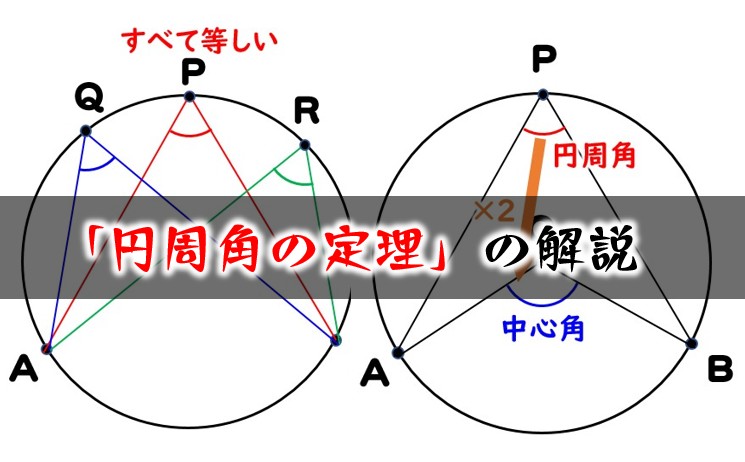



円周角の定理の解説 問題の解き方 数学fun




円周角 Wikipedia




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円周角の定理の基本 計算 無料で使える中学学習プリント




円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




中3 数学応用 円周角の定理 証明 中学生 数学のノート Clear



円周角の定理と中心角 中学3年数学 Youtube




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円周角の定理とその逆 思考力を鍛える数学



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




勉強しよう数学 使い易い形の拡張円周角の定理と円周角の定理



円周角



円周角の定理 練習問題 苦手な数学を簡単に



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



円周角の定理の逆の証明



円周角の定理 練習問題 苦手な数学を簡単に




中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生




数学 中3 57 円周角の定理 少し応用編 Youtube



1



円周角



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
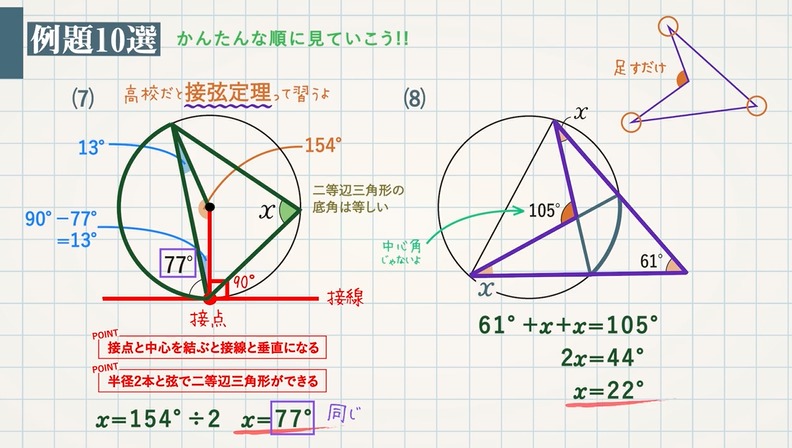



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
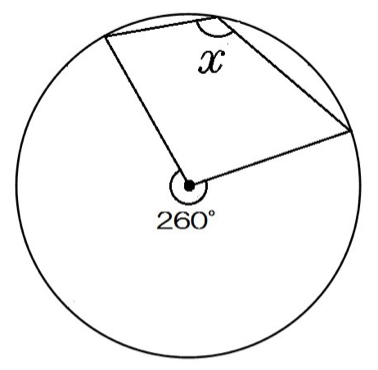



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
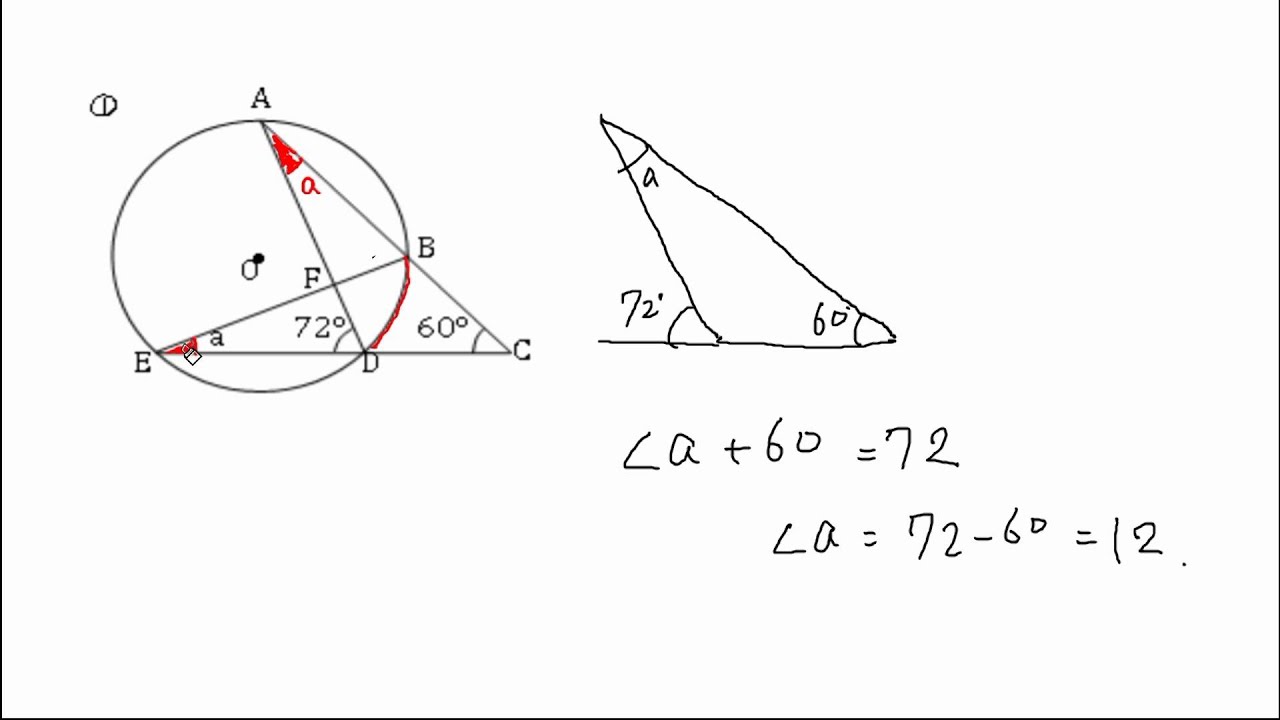



円周角の定理 問題 Youtube



円周角と中心角 中学から数学だいすき




円周角の定理の逆 無料で使える中学学習プリント
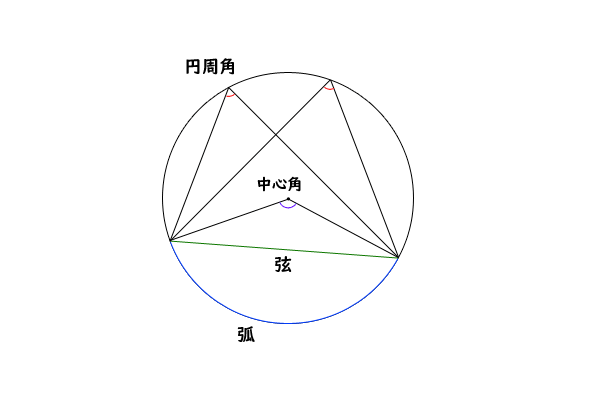



円周角の定理とその逆の証明 高校数学マスター
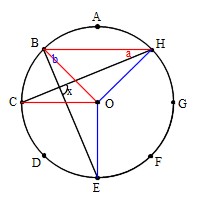



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



円周角の定理



1




勉強しよう数学0 11




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4




円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典
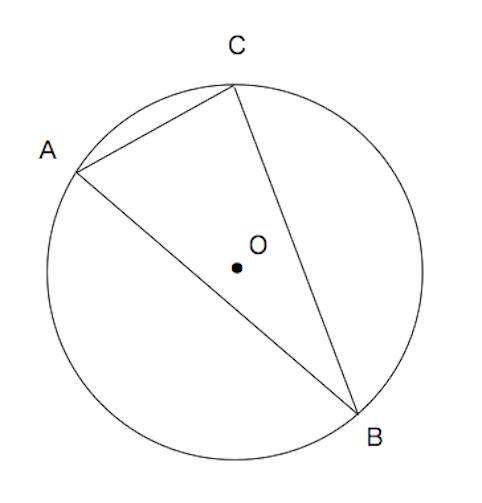



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に




円周角と円の外の点を結んで おときち副塾長 電脳空間学習塾かもん Youtube




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube
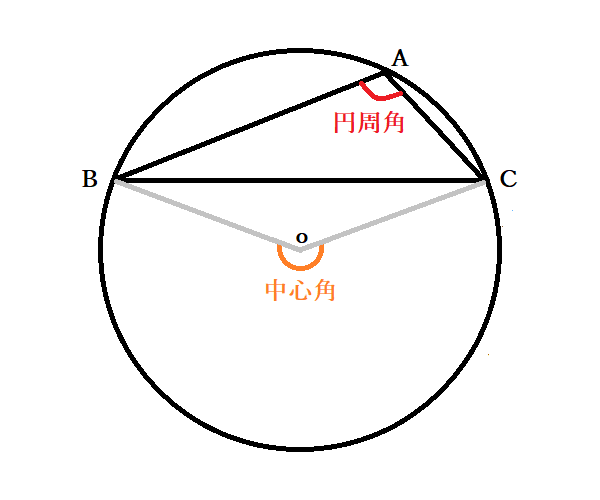



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog
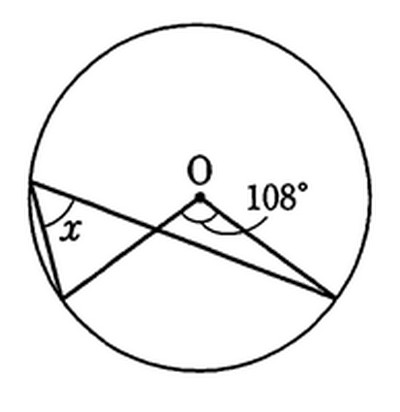



円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
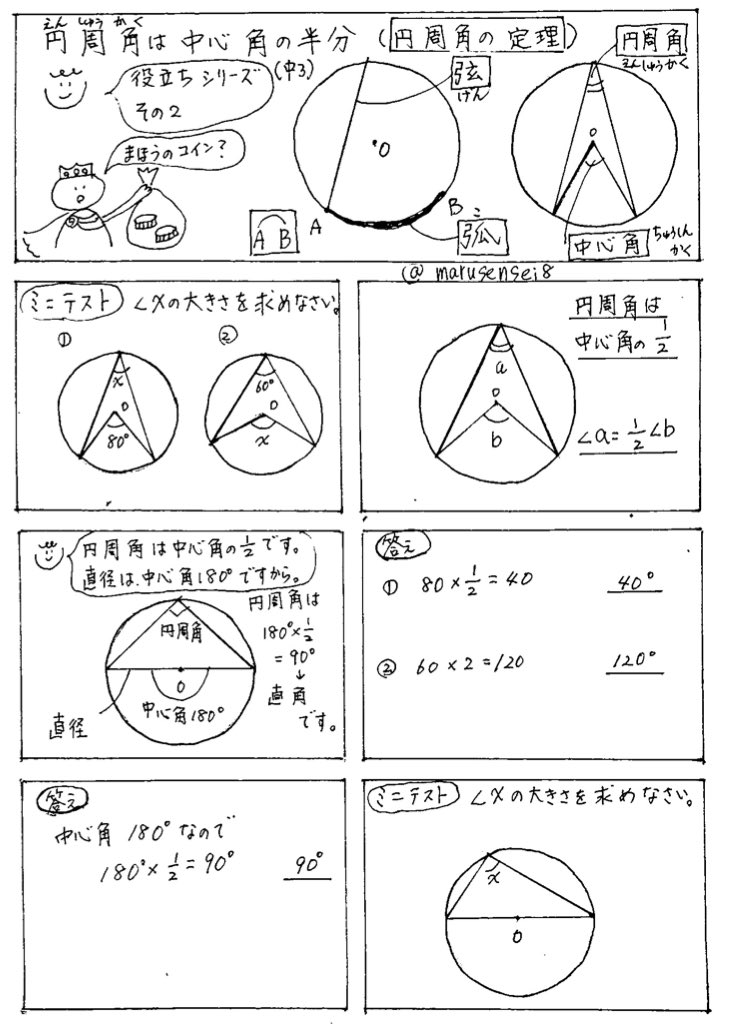



円周角の定理




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
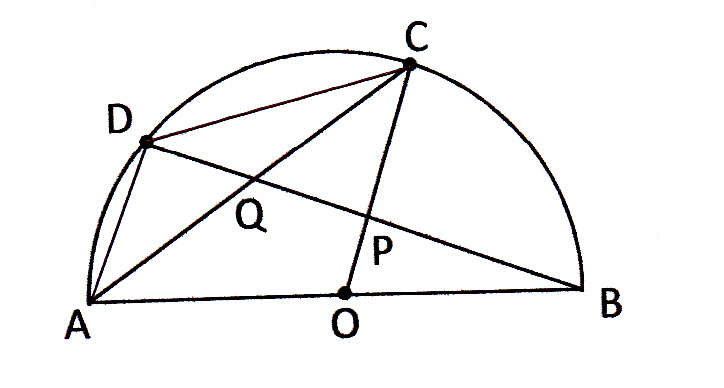



円周角の定理を使った相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
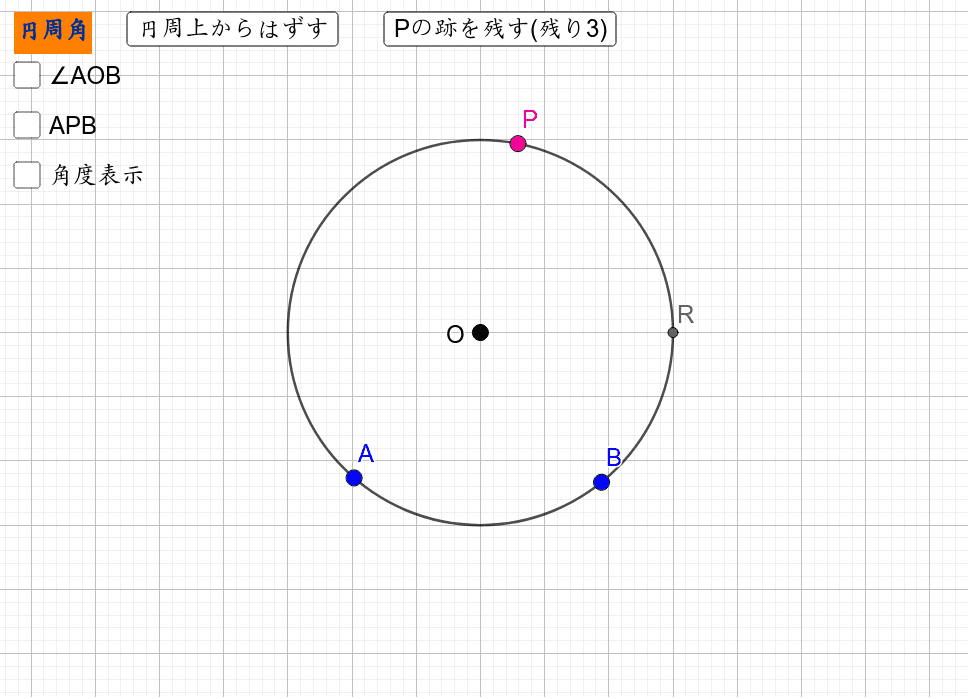



円周角の定理の発見 Geogebra



円周角



円周角の定理




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
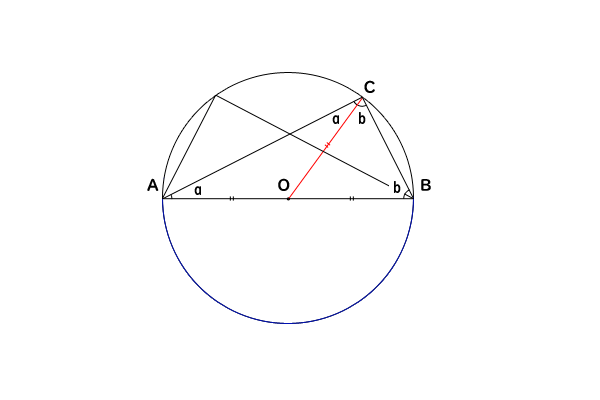



円周角の定理とその逆の証明 高校数学マスター



円周角の定理




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




高校数学a 共円条件 4点が同一円周上にある条件 受験の月
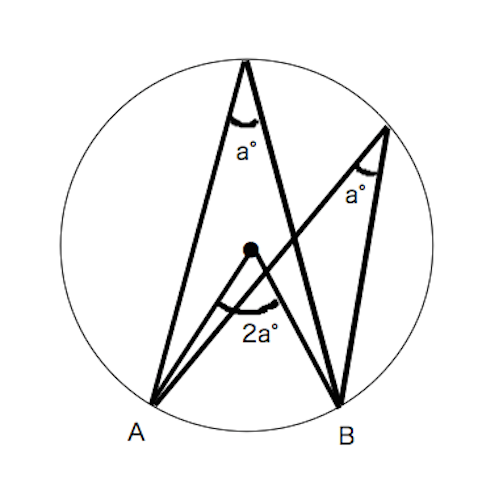



円周角の定理 苦手な数学を簡単に



円周角




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




数学 中3 56 円周角の定理 基本編 Youtube
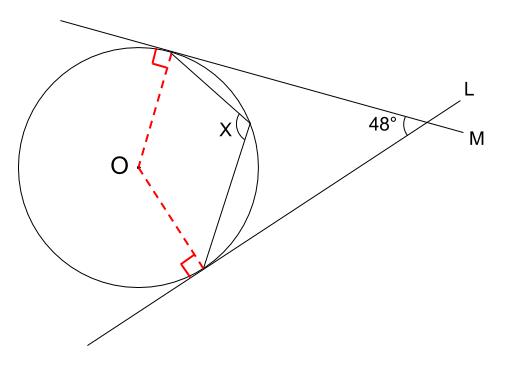



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



1
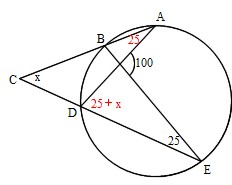



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円と三角形 角度 中学から数学だいすき




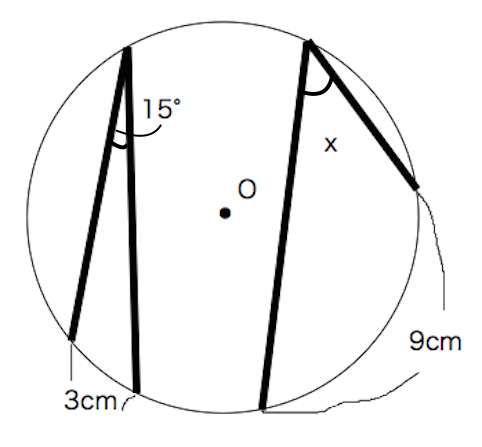
円周角の定理です Xの角度の求め方を教えてください Clear




接線と円の関係 Jsciencer



1



0 件のコメント:
コメントを投稿