直径から計算 直径: 面積: 半径から計算 半径: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形三角比で三角形の面積を求める方法の証明 ABCにおいて、次の公式が成り立つ。 この公式の証明をしていく。 証明 Cから辺ABに対して垂直に線をおろし、その交点をHとする。わかりやすくするために、AC=b、AB=c、CH=hとする。 A球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
梯形面积公式求下底 不规则求梯形面积公式求不规则梯形的面积的公式 尚书坊
面積 公式 小学生
面積 公式 小学生- 東大塾長の山田です。このページでは、「積分の面積公式」について解説します。積分で面積を求める有名な公式「1 / 6公式」,その他にも,曲線と接線の間の面積を求める「1 / 3公式」,「1 / 12公式」についても詳しく解説しているので,ぜひ勉強の参考にしてください!側面積の公式が「2πrh」なので混同しやすいです。間違えないよう注意しましょう。円柱の体積の求め方は下記も参考になります。 円柱の容積は?1分でわかる意味、求め方と式、表面積の計算、体積 まとめ 今回は円柱の側面積について説明しました。意味や求め方が理解頂けたと思います



小学数学图形的周长 面积 体积公式 孩子学习必备 周长 体积 圆柱 新浪新闻
四角柱の底面積は「台形の面積」を求めましょう。 四角柱の底面積= (46)÷2×5=25cm 2数学Bのベクトルまでで,大学受験で最低限必要な三角形の面積公式が揃いますので,以下にまとめます. 空間ベクトルまで既習だとこのページがすべて理解できます. 目次 1: 高校数学で必要な三角形の面積公式まとめ 2: 例題と練習問題 高校数学で必要な三角形の面積公式まとめX 囲まれたグラフがどこの位置に あろうと常に上下で求めること ができる! S x=β x =β =β β x x =β =α α α β x y = ax2 qx r y = px2 qx r y = ax2 bx c y = ax2 bx c y = ax2 bx c y = ax2 bx c x =αβ 2 = (βα) a
3 12分の1公式(Part1) 右の図のように,放物線と2本の接線とで囲ま れた部分の面積を求めるときに使用する公式で ある。 例題3放物線上の2点A,Bのx座標をそれぞ れα,βとする。2点A,Bにおける接線の 交点のx座標を求めよ。長方形の面積 平面図形 公式 集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 四角柱 四角錐 三角柱 三角錐 円柱 円錐 空間図形 公式集 確認シート a=長さ b =長さ h=高さ ℓ=弧の長さ S =面積 V =体積 Created Date 9/2/08 AMAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
円の面積の求め方 公式と計算例 Scipursuit 面積の求め方 円 円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314 中学生以上では、文字を使って次のように書きます。 S = πr2 S = π r 2 半径 r の円どれもこれもひし形の面積公式を使って $$(対角線)\times (対角線)\div 2$$ これで計算することができるよ(^^) なぜ対角線をかけるの? ひし形の面積を求めるのに、なぜ対角線を掛けるのか? それはね ひし形の面積を求めるために次のような図形を考えているからなんだよ! 対角線を引くと円の面積を求める公式は小学校で習いますが、なぜその公式になるのか?という 疑問 (ぎもん) は、高校2年生で 微分 (びぶん) を学習するまで分かりません!下のリンクでは、図形的に公式を 理解 (りかい) してもらう方法を 紹介 (しょうかい) しています。 扇形 (おうぎがた) の面積も 重要



三角形面积计算公式 三角形面积公式 越多越好 100查分网



面积公式大全图片 搜狗图片搜索
四角形の面積 ・正方形の面積 1辺の長さから正方形の面積を計算します。 ・長方形の面積 縦と横の長さから長方形の面積を計算します。 ・台形の面積 上底と下底、高さから台形の面積を公式を使って計円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き 円の面積 面積; ・台形の面積を求める公式として「(上底+下底)×高さ÷2」にまとめられることをおさえる。 4.チャレンジ問題を解決し、学習内容を活かす (1)別の台形でも、公式が適用できるかどうかを確かめながら、チャレンジ問題をする。 ・1辺が高さになっている場合や不安定な位置におかれて




三角形公式面積三角形面積公式 Utvos



圆周长及面积计算公式 已知圆周长求面积公式 老兵医疗救护
土地の面積を変えないため、2.で求めた面積を用いて、次の式を組み立てる。 ここで、1.において、計算の都合上座標値を移動しているため、これを加えると次のようになる。 + 112 = 560 よって、点GのX座標は、560 mとなる。 解答:3 E D C B A F G 道 路 (0000,0000) 道 路 (0000 三角形の面積にまつわる公式 ヘロンの公式 まずはおなじみ,三角形の三辺の長さから面積を求めるヘロンの公式。 外接円の半径と三角形の面積の関係 S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c 公式。これもなかなか使い勝手が良い公式。応用としてオイラーの不半径から円の面積と円周を計算します。 = 面積 s 円周 l お客様の声 アンケート投稿 よくある質問 リンク方法 円の面積 110 /35件 表示件数 1 1501 歳未満 / 小・中学生 / 非常に役に立った / 使用目的 計算 ご意見・ご感想 複雑でよく間違える計算なので



梯形面积公式 用2种拼组 2种分割 1种割补法
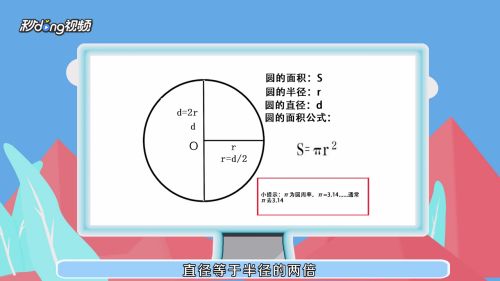



圆的面积公式怎么算 百度经验
/ 数学公式集 / 面積;解答: (1)5×8=40 答:40平方公尺。 (2)21÷7=3 答:3公尺。 平行四邊形的面積公式 (1)的flash練習 計算左圖平行四邊形的面積為多少平方公分? 計 算 左 圖 平 行 四 邊 形 的 面 積 為 多 少 平 方 公 分 ? 解: 邊和 邊都可以當底,但 邊沒有給相對應的高三角形の面積公式 まとめ 今回は数学Ⅰの三角関数からsin(サイン)を用いたについてまとめました。 他にも、教科書に内容に沿ってどんどん解説記事を挙げていきます。 お気に入り登録しておいてもらえると、定期試験前や入試勉強をするときに確認できます。 ここまで読んでくださって




三角形正多边形面积公式 三角形png图片素材免费下载 图片编号 Png素材网




例題 長方形面積公式的應用 數學 均一教育平台
求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 a=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正この公式により π が無理数であることが分かる。 1663年 値 村松茂清 が『算俎』を著し、円に内接する正 2 n 角形 (2 ≤ n ≤ 15) の辺の長さから π ≒ 692 48 とし、小数点以下7桁まで正しい値を求めた。 「なんでこの公式で円の面積が求まるんだろう?」と感じる方も多いのではないでしょうか。 そこで今回は「なぜ円の面積が半径×半径×314になるのか」を見ていきましょう。 photo credit Travis Wise スポンサーリンク 円の面積の求め方を図でイメージしてみよう まず、半径2cmの円を10等分し



三角形面积公式x54 小学入门易大学精通难难度三星 哔哩哔哩 Bilibili



小学数学图形的周长 面积 体积公式 孩子学习必备 周长 体积 圆柱 新浪新闻
公式集 - 数学 図形・面積・体積 スポンサーリンク 数学ハンドブック 数学-公式集 スポンサーリンク 物理学ハンドブック 物理学ハンドブック 構造計算プログラム 公式集-断面性能 記号-単位 ちょっとよりみち 図 式 扇形 A = 面積 L = 円周の長さ R = 半径 扇形 A = 面積 L = 弧 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるのだろうか。 様々な証明方法があるが、まず它的面積是多少平方厘米? 步驟(1) 選擇公式 圓的面積 = πr2 步驟(2) 代入公式 = 314 × 42 步驟(3) 計算過程(不能跳步) = 314 × 16 步驟(4) 注意單位 = 5024(平方厘米) 步驟(5) 列出答句 答:它的面積是5024平方厘米。 二、計算題。




小學所有的數學 圖形的計算 公式 每日頭條



圆面积公式大全 三角形面积计算公式大全及练习题 尚书坊
面積は当然、底辺×高さ×\(\frac{1}{2}\)で求められるので、以下の通りです。 \begin{eqnarray}S=6×3\sqrt{3}×\frac{1}{2}=9\sqrt{3} cm^2\end{eqnarray} こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。 面積 面 積 = 4 × 4 = 16 c m 2 「たての長さ 3 c m,横の長さ 5 c m の長方形」は 面積 面 積 = 3 × 5 = 15 c m 2 となります。其中一個定義面積的方法是利用 公理 定義。 面積 可以定義為一個由所有( 可測 )平面圖形組成的 集合 M 映射至實數的函數 a ,並滿足以下條件:



圓公式面積 觀念 圓面積計算公式的推導 Eyflka




三角形面积公式 三角形面积公式盘点 52fmz购物网
外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して




圓的面積單位圓的面積公式 Gjlni
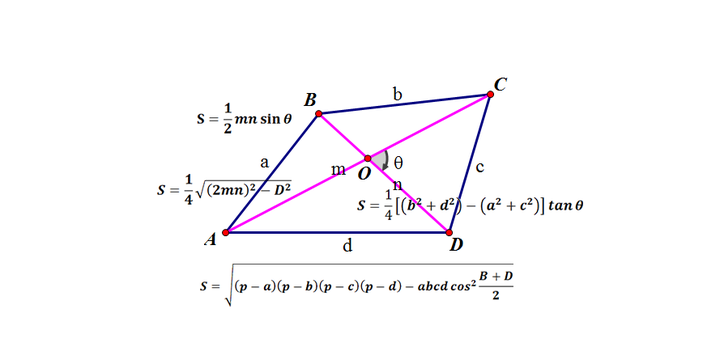



四边形的面积公式 知乎



棱柱的侧面积公式直棱柱的侧面积 全面积怎么求 麦税尼网



图文版 小学数学图形的周长 面积 体积公式 圆柱
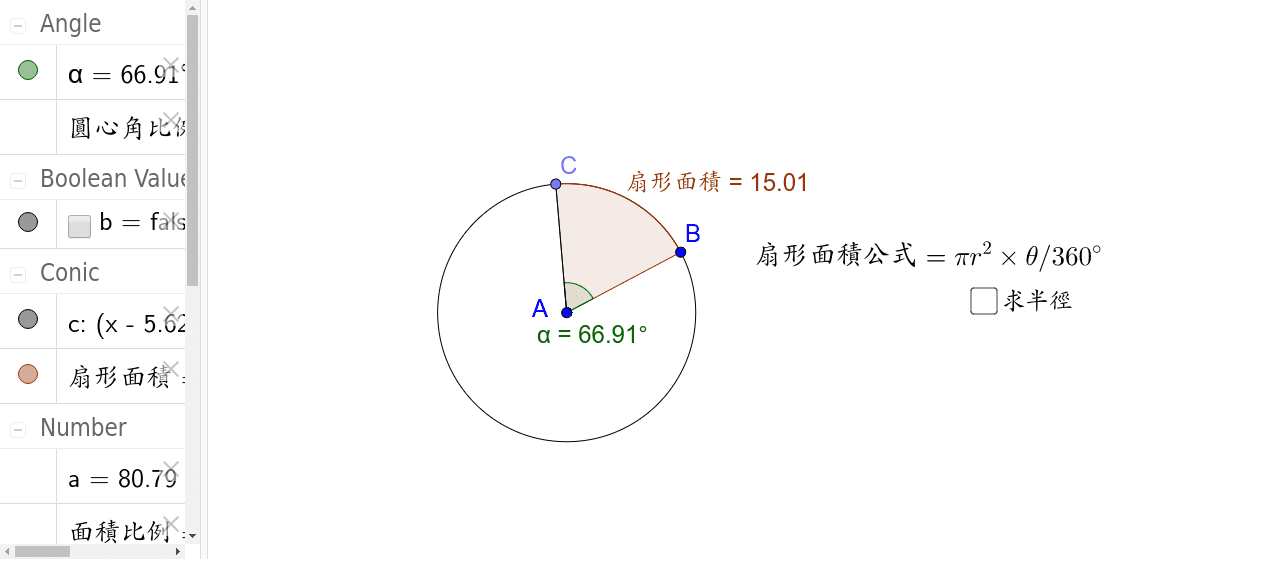



扇形面積公式2 Geogebra




菱形面積公式 菱形面積公式就是由三角形面積公式得來的 菱形面積 兩個三角 百科知識中文網




小學必會圖形求面積10法 家長收藏版 每日頭條
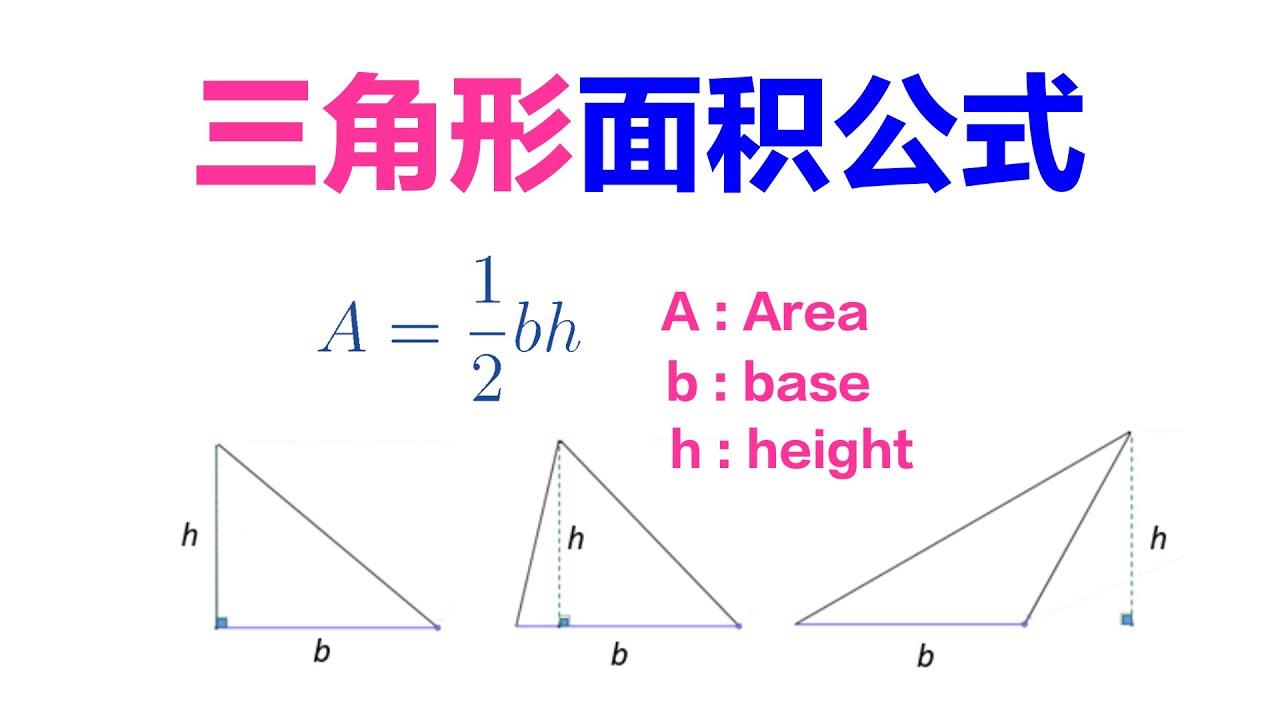



三角形面积公式的证明 Youtube



锥形面积公式怎么计算圆锥的面积 用什么公式 朵拉利品网




初中數學幾何圖形常用面積算法 趕緊收藏 每日頭條




十七种三角形面积公式



三角形面积公式余弦定理 快懂生活




三角形的表面积公式 西瓜视频




股票一个区域画阴影公式 数学几何阴影面积公式 天空财经




直角三角形公式面積 直角三角形的面積公式是什么 作業幫 Jvvx
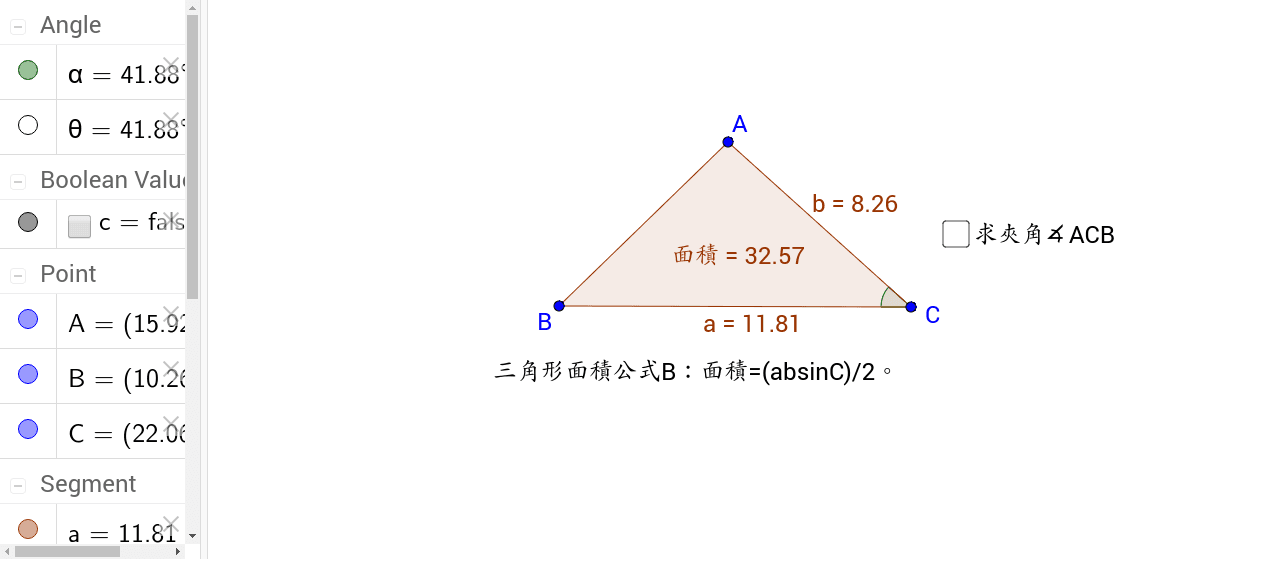



三角形面積公式b2 Geogebra



計算弓形面積 台北市立陽明高中數學科




三角形的面積



等边三角形面积公式表 等边三角形面积计算 七月seo




扇形面積公式 公式 推導過程 注意事項 中文百科全書



梯形体积公式梯形体积公式 一加一



Q Tbn And9gcrc0zk5rndihxchrex0elksjk4vngxujtpo6ofscvvgs5perp6k Usqp Cau



图文版 小学数学图形的周长 面积 体积公式 圆柱




三角形的面積
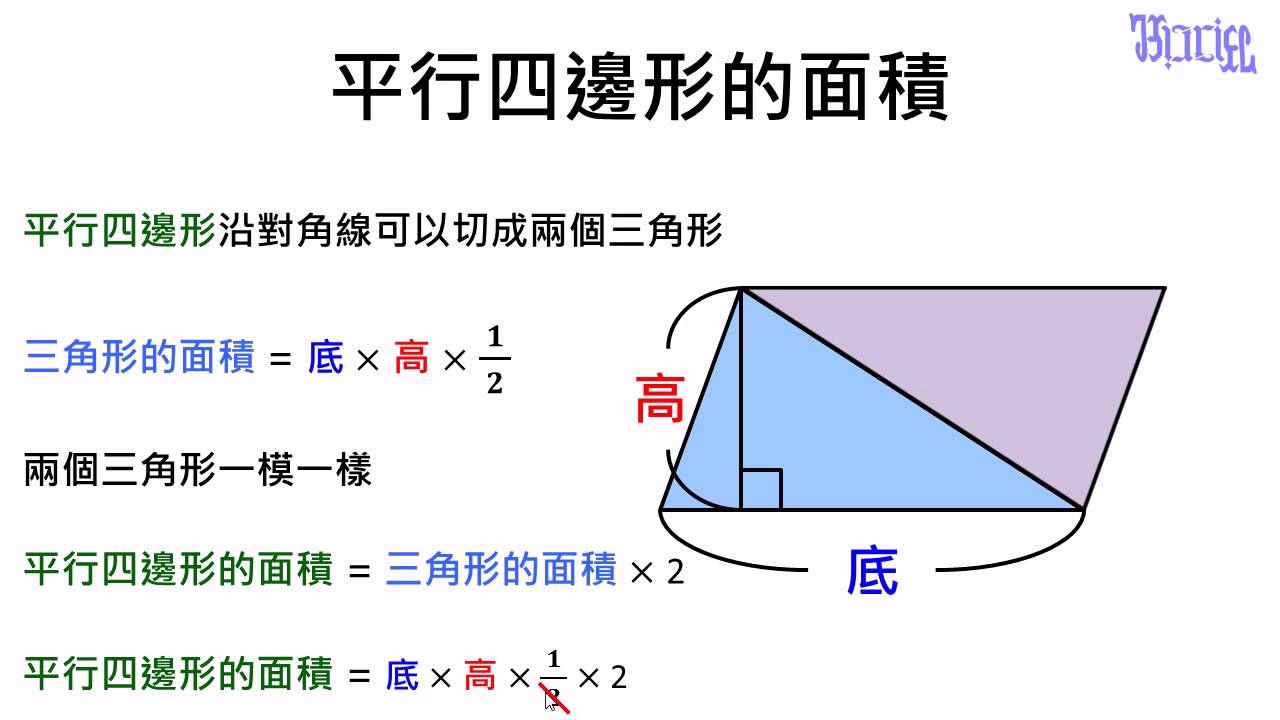



面積 04 平行四邊形的面積計算方式證明1 Youtube



小学生五年级面积公式 西瓜视频搜索



扇形面积面积公式 体积 表面积计算公式大全 尚书坊




面積問題 小奧的孩子也看過來吧 秒殺初中生 每日頭條
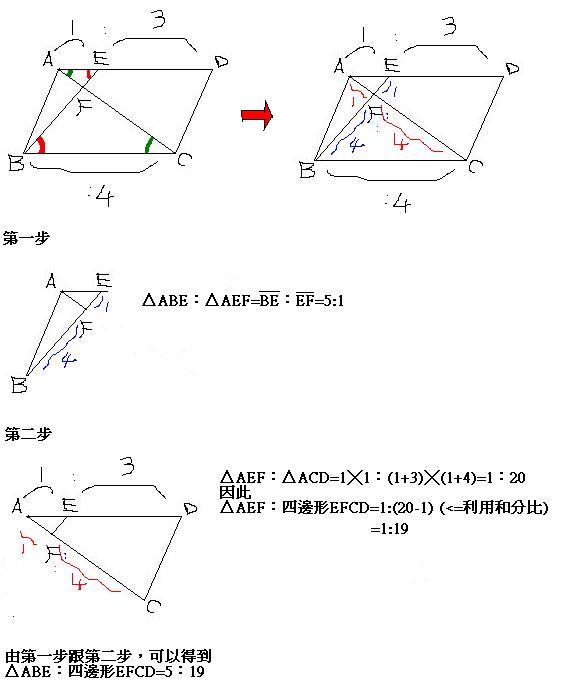



例題 三角函數 三角形面積公式 Iii 平面坐標與向量 高中的數學 Math Pro 數學補給站




圓柱面積公式表面積 Bosswu




三角形的面积公式小学



三角形面积公式 快懂百科
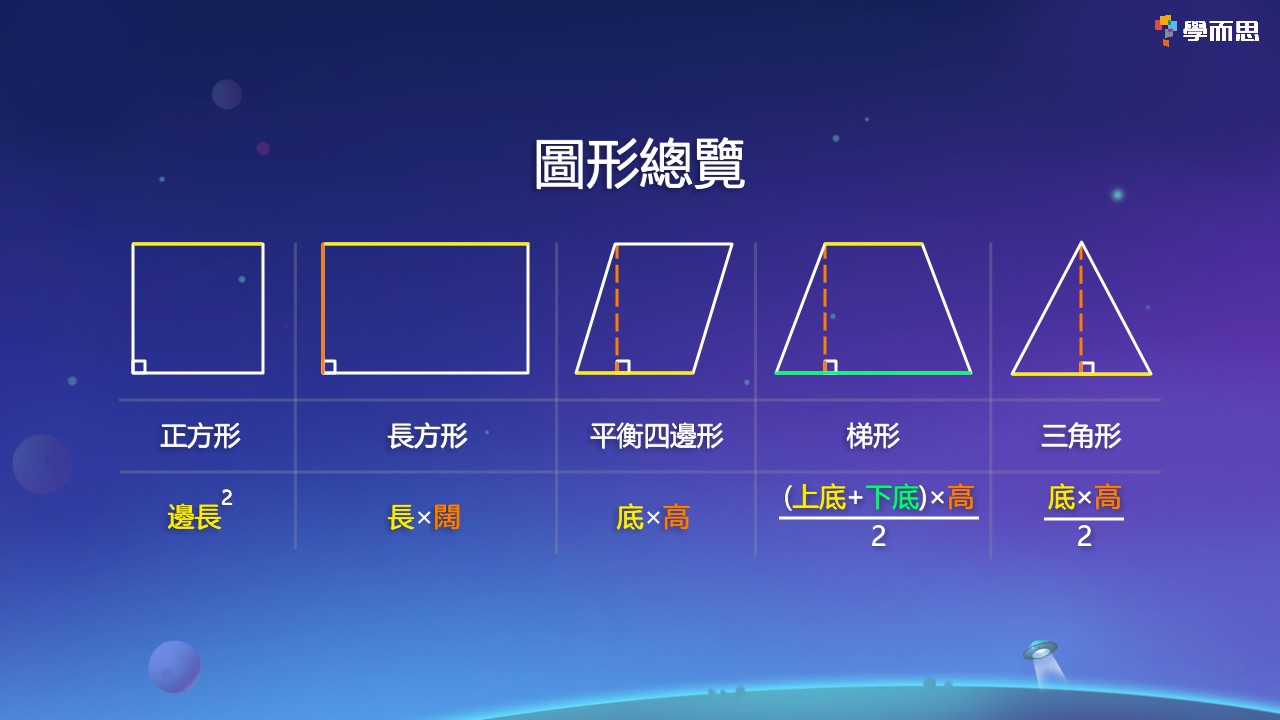



呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港



圆的面积计算公式 圆的面积计算公式画法



梯形面积公式 用2种拼组 2种分割 1种割补法



用海伦公式求三角形面积 只知三角形三条边分别是3 5 6 如何求三角形面积 哔哩哔哩 Bilibili




数单位正方形求面积计算公式 视频 长方形 正方形面积的计算 可汗学院



三角形面积公式 玄数



S扇形面积公式大全 万图壁纸网



面积公式大全小学数学必背公式全集 面积计算



1



7 4 平行四邊形的面積公式 高市資教中心教材網



四边形面积公式 面积最大值问题 哔哩哔哩 つロ干杯 Bilibili



1




梯形面积公式是什么梯形面积怎么计算 传承网



体形面积公式初中数学公式 圆柱体面积公式 女士吧



三年级数学平面图形的周长 面积公式汇总 小初高题库试卷课件教案网
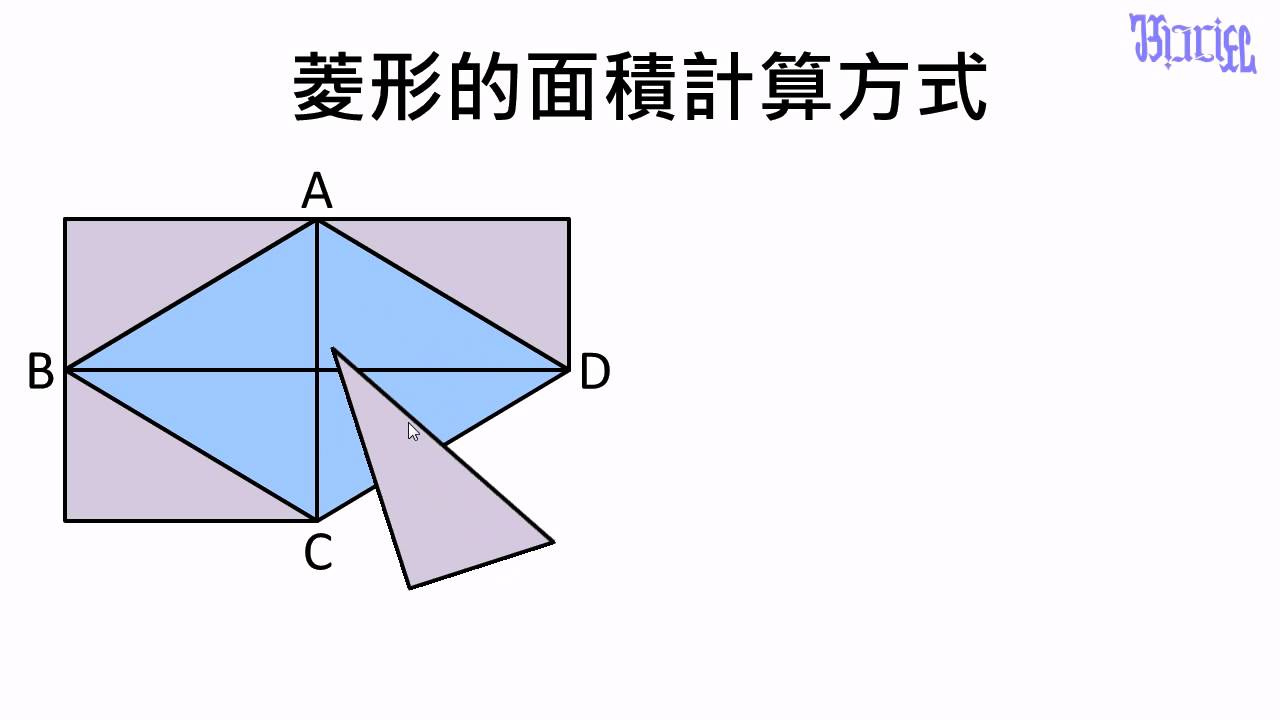



面積 14 菱形的面積計算方式 Youtube




梯形面積的由來 紀算 補習班 數學補習班 三重 文理補習班 數學公式 數學題庫 數學競賽 國小數學 國中數學 痞客邦



1



梯形面积公式求下底 不规则求梯形面积公式求不规则梯形的面积的公式 尚书坊




圓的周長面積公式圓的面積公式和周長公式 Ycww




常用圖形求面積計算公式 人人焦點
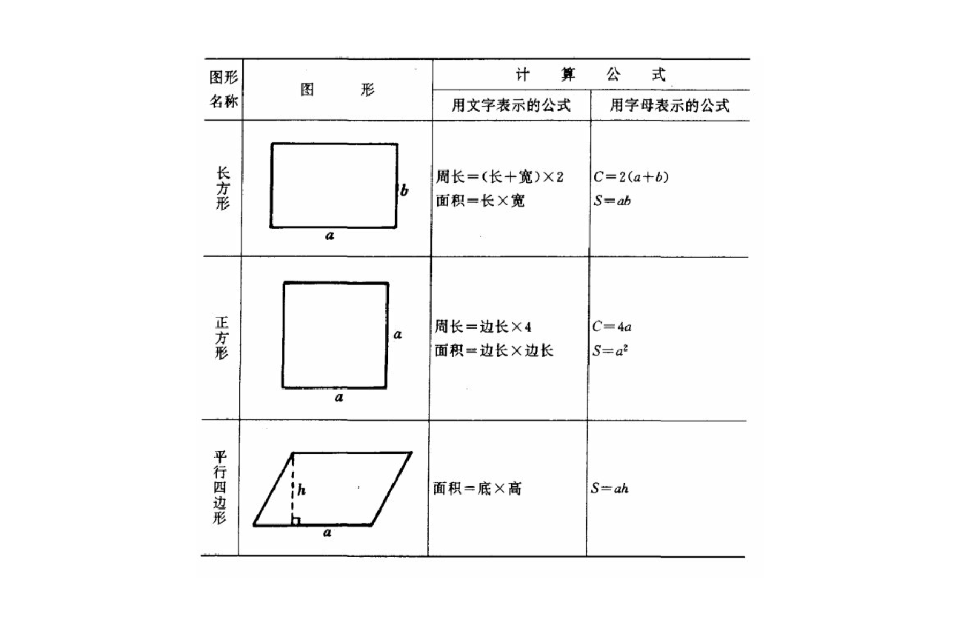



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



矩形面积公式 三角形的面积公式 尚书坊



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊




三角形面积公式 三角形面积万能公式 十安知识网
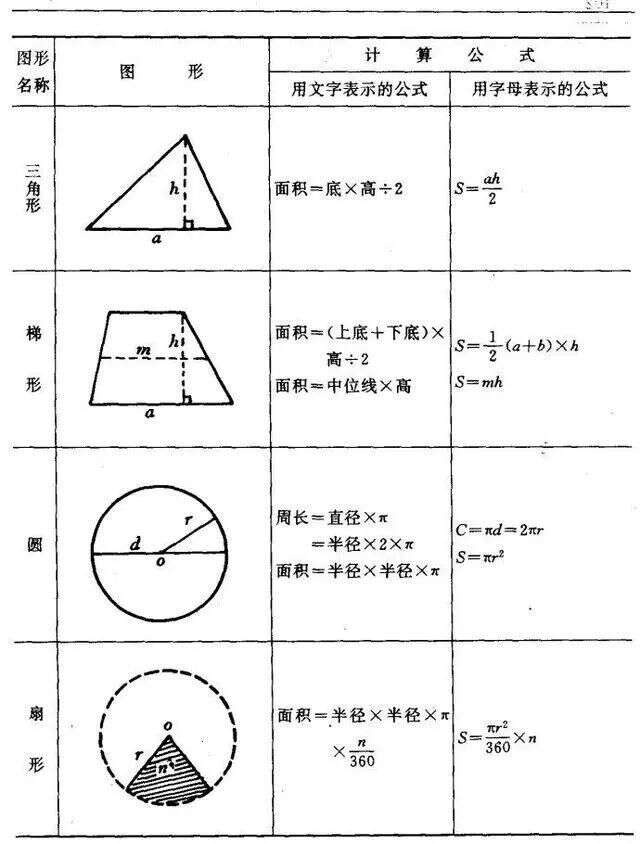



小学数学图形的周长 面积 体积公式 孩子学习必备 楠木轩




基礎 長方形 正方形的面積公式 數學 均一教育平台
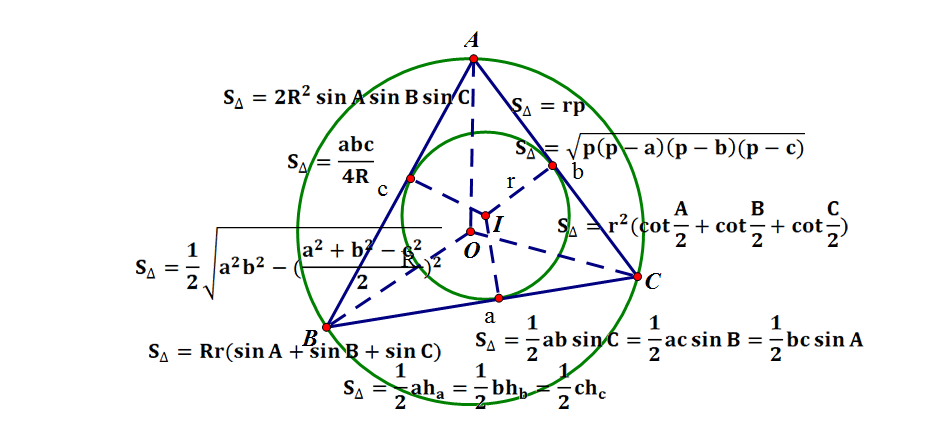



从三角形的面积公式谈起 知乎




08 長方形面積公式的應用 Youtube




任意三角形面积公式是什么



梯形面积计算公式 梯形面积计算公式画法
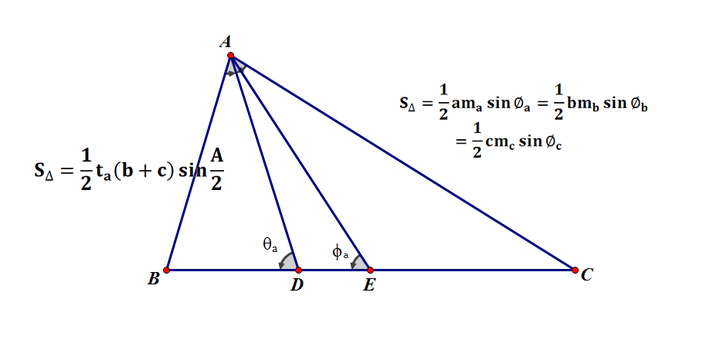



三角形的面积公式七叙 知乎




圓的面積公式圓的面積公式 高三網 Qqkaii




圆的面积公式 圆的面积公式是什么 517鲜花



圆面积计算公式是什么 圆的截面积公式是什么 尚书坊



平行四边形的面积公式 聚热点网




不平行四边形面积计算公式与在线计算器 三贝计算网 23bei Com



菱形面积公式 万图壁纸网




圆的体积计算公式图解第1页 驾考预约大全



什么 任意四边形也有面积公式 海伦公式的推广及讨论 哔哩哔哩 Bilibili



梯形面积公式 用2种拼组 2种分割 1种割补法



半圆周长和面积的计算公式 学习岛



圆锥的底面积公式是什么圆锥的底面积公式是什么 朵拉利品网




弓形面積公式弓形面積計算器 Qwvatk




5下面積概念題2 6菱形面積 Avi Youtube



弓形面积公式 万图壁纸网




梯形面积计算公式



圆面积的计算公式 圆的面积公式是怎么得到的 图文 叽叽歪歪吧
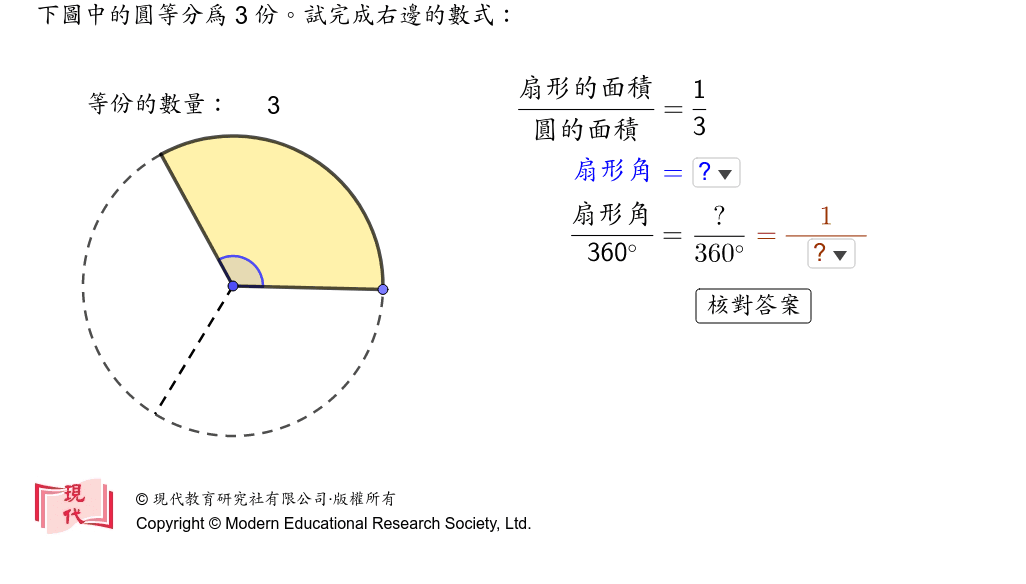



扇形面積公式 Geogebra



平行四边形的面积公式 平行四边形的面积公式画法




體表面積表初中數學 幾何 面積與體積公式 Uhlwc




常用求面积 体积计算公式 豆知网



三角锥形面积公式三角形的体积公式是什么 银颜网
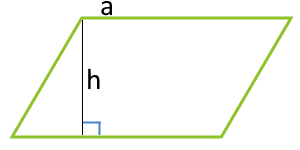



平行四邊形的面積




十大家装公司 梯形面积公式 梯形面积怎么计算 合抱木装修网
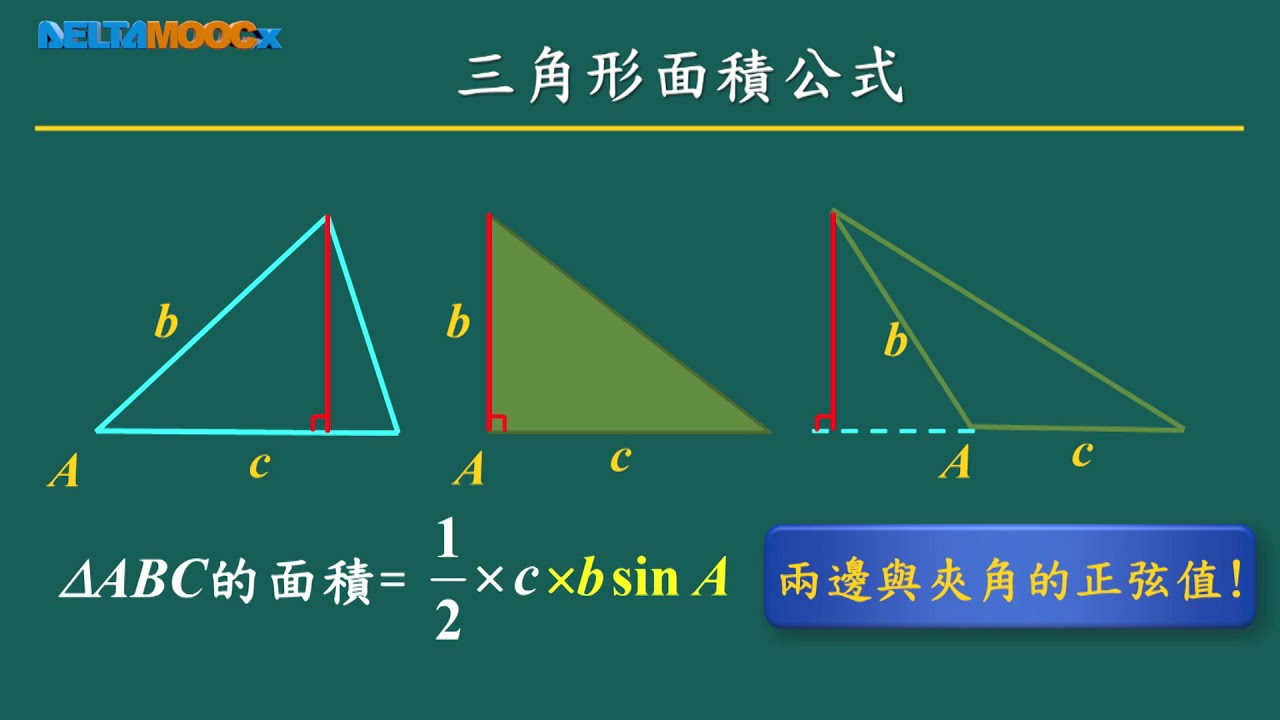



高中數學 三角函數 正弦定理與餘弦定理 1 三角形面積公式 吳汀菱 Youtube




面积公式 搜狗百科
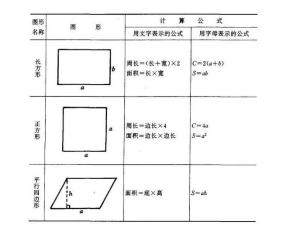



面积公式 搜狗百科



0 件のコメント:
コメントを投稿